


 |
3. Model Generation with Poses++ | 
 |
 Introduction
into Model Generation
Introduction
into Model Generation
 Modelling
Concepts of Poses++
Modelling
Concepts of Poses++
Predicates
Transitions
Arcs
Modules
| 3.1. Introduction into Model Generation | 

 |
Model generation in terms of simulation technology means the reproduction of a real or fictive system which is to be investigated in the form of a model, using the descriptive means of a simulation system.
The descriptive means of Poses++ simulation system is rule based and derived from predicate-transition-nets. Poses++ is not a Petri-Net-Tool in the first place. It is a modelling and simulation environment suitable for small and complex discrete, discontinous and also continous processes. But the modelling is based on principles of petri net definitions.
The generation of a model firstly requires an exact analysis of the system
to be reproduced:
 |
What are the real essential components of the system and what are the system's states occurring due to these components? |
 |
How to reproduce the system's behaviour in a way that is adequate and evaluable? |
The information gained this way are then defined by means of modelling elements. Poses++ describes the system states by means of predicates which are buffers containing stored data representing informations or physical objects, and the system behaviour by means of transitions which are rules describing the situation and the kind of changes in predicates. Changes in the net i.e., changes of the model situation are caused by the activities of transitions whereas existing data are destroyed and new data are created. The manner in which data are destroyed and created is determined by directed arcs which relate predicates and transitions to each other. So the arc expressions define the rule parts according to which a transition is activated and a new model situation is to be created.
Example: Traffic light control.
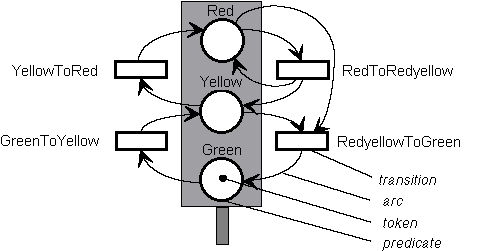
The example shows three predicates (Red, Yellow and Green) which represent the possible states of the model. The data contained in the predicates describe the current state of the model. These data are called tokens. Now the predicate Green is marked with a black token and, thus, the state "green traffic light" is reached. A change of token situation (also called: marking set) which results in a change of the state is made by the transitions GreenToYellow, YellowToRed, RedToRedyellow and RedyellowToGreen. A transition is only activated when all descriptions of the situation given by the adjacent arcs are relevant. This situation is also called: the transitions has concession. The process when a transition changes the state of the model is called: "the transition fires". In the example only the transition GreenToYellow can change the current model situation because the incoming arc of the transition destroys a token in the predicate Green while its outgoing arc simultaneously creates a token in the predicate Yellow. This change of the token situation results in the new model state "yellow traffic light". Based on this state the transition YellowToRed meets the requirements of the fire rule next. In this way all switch positions of a traffic light can be simulated one after the other. Accordingly there are four different switch positions or model states in this example:
All model states and their transitions can be represented graphically by means of a state machine. The complete state machine for the traffic light example is represented by the following condition event net (the simplest form of a predicate transition net):
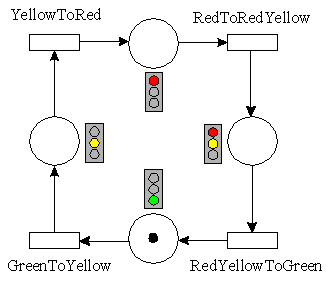
There is always one but only one state in a state machine which is marked or activated and is therefore considered to be the current model state. In the above graph the GreenTrafficLight contains the valid black token. Regarding its possible states this graph could be expanded. The state GreenYellowTrafficLight could be inserted, for example, between GreenTrafficLight and YellowTrafficLight. But in doing so, a single token would be confronted with a continuously growing net structure. So the question is whether the valid model states must be expressed through individual predicates or not. Why not indicate the respectively current model state by means of a predicate called traffic light state ?
The information which was represented before by various predicates describing the possible states of the model is now expressed by the content of a single predicate called TrafficLightStatus. In order to allocate the necessary information to the tokens themselves, distinguishable tokens must be available.
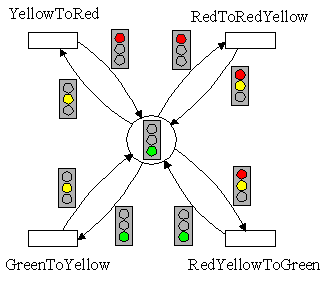
For this purpose it is not sufficient to use the black token such as the state token in the state machine as an information carrier for binary yes/no decisions. A token in the predicate TrafficLightStatus should be able to accept all possible traffic light state in data (green, yellow, red and red/yellow). Such a token is called an attributed token. The situation of the model will now be represented by the predicates with token and the actual token values. This situation can only change when a transition fires within the net. The current token value green of the predicate TrafficLightStatus is only changed when the transition GreenToYellow fires. In order to make the transition fire, the requirements of its rule must be met. In the case of the transition GreenToYellow the following conditions have to be fulfilled:
| and |  |
The predicate has to contain a token with the value green. This is symbolized by the green traffic light as an arc expression (arc directed from the predicate TrafficLightStatus to the GreenToYellow transition). |
|---|---|---|
 |
A token with the value yellow can be filed in the predicate. This is symbolized by the yellow traffic light as an arc expression (arc directed from the GreenToYellow transition to the predicate TrafficLightStatus). |
A complete imaging of the model states by corresponding token value allocation is one extreme in model generation. The other extreme would be the state machine in which every possible model state is represented by a predicate. As always in cases of extremes, the ideal solution lies somewhere in the middle between both modelling approaches. Thus, the traffic light control represented above is an example in which the model generated is very close to reality.
When developing a simulation model which shall be close to reality, the model designer has the complicated but challenging task to detect the essential states and activities, as well as their interdependencies in the system to be simulated, and to describe them by means of net elements and rules.
Model |
||||
rules and activities |
parts of the rules |
states |
objects and data |
|
|
|
|
|
|
| Transitions | Arcs | Predicates | Black Tokens |
Attributed Tokens |
The most complicated part in it remains the necessary abstraction beginning with the presentation of the problem of the system to be investigated up to the adequate simulation model. This often takes a lot of painstaking work to get all of the necessary information together. These tiny details have a decisive influence on the result and on whether the model really behaves the same way as the original does. Therefore the following guidelines should be roughly observed when generating a model:
General Guidelines for Model Design
Information on causal connections and dependences should be recorded as completely as possible. Redundant information is even advantageous because lack of clarity can be eliminated with their help. In later stages it is often necessary to make assumptions about the real system. Then the success may depend on information which seemed to be unimportant before.
When designing a model, the total complex system should be divided into clearly understandable components (modules) which can be implemented independently of each other, and to describe their relations and interfaces. Such a division is called modularization. You should not only devide physical parts of the system to be simulated in modules but also methods or behaviour sequences of objects in the same context you should express separeted.
The advantages of this design method are, among others:
 |
clear and understandable model design |
 |
distribution of tasks among several module designer |
 |
repeated use of existing modules |
 |
replacements of modules during maintenance of large models |
 |
limitation of details which a user needs to know about a module |
Precise reproductions of the real system structures by the model result in a more understandable and applicable simulation model. In addition to that it is possible to use the simulation models as a base for discussions with other partners because important details can also be detected by uninitiated spectators.
In most cases it is necessary to create an animation layout according to the system conditions in order to represent concise processes of a running simulation experiment. Often there is no other possibility for the "parallel" realization of several system situations and, thus, for the visual check of model correctness. Also the acceptance of the results of simulation experiments is raised by means of animation.
Definitions concerning essential decisions in model designing should be documented sufficiently because only in this way is it possible to retrace an already reached stage of model development.
Good model designs distinguish themselves by clear and logical structures and flexibly adjustable parameters. Selected standard values of parameters should be usable in the majority of applications. The quality of model generation decisively increases the possibilities and variants of executable simulation experiments and, thus, the lifetime of the model.
| 3.2. Modelling Concepts of Poses++ | 

 |
The first abstraction of small systems to be reproduced in a model is mostly a graphical net with verbal descriptions. Such an approach permits the model to be checked for its completeness and correctness with regard to reality. Then the model is designed by means of descriptive elements of a simulation system for the purpose of detailed evaluations on the simulation model. Using Poses++ to implement a graphical model design based on nets is relatively formal because the describing structure is based on predicate-transition-nets. If you model more complex and large systems it is often easier to imagine the transitions and their contexts as rules like verbal descriptions of a system instead of breaking pencil sharps on large drafts.
Predicates
Transitions
Arcs
Modules
| 3.3. Modelling Example | 

 |
The philosophers' problem is a classic example of explaining parallel processes
and related terms such as deadlock (blocking) or mutual exclusion (starvation),
or explaining utilization strategies of global ressources etc. Simultaneously
the problem illustrates how difficult it is sometimes to understand even
very simple parallel structures.
 |
Five philosophers sit together at a round table. Each philosopher devotes himself to meditation for a certain time until he gets hungry and starts to eat. After eating he meditates again etc. Each philosopher has his own plate. Between pair of two plates only one chopstick lies. In order to eat, the philosophers compete with their neighbours for the chopsticks lying left and right to them respectively. All chopsticks represent global ressources in this system. Therefore the access to a chopstick is always a critical stage which must be globally synchronized in order to solve the conflicts (e.g. two philosophers reach for the same chopstick simultaneously). Blockings can also arise when all philosophers get hungry at the same time and grasp their left chopsticks simultaneously. Thus all chopsticks are occupied and none of the philosophers can start to eat. Also mutual exclusions are possible i.e., some of the philosophers are disadvantaged in the distribution of the chopsticks. This strategy of discrimination in distributing global ressources is also called starvation. |
These classic problems of parallel processes can be eliminated from the very beginning by using Poses++ as the model describing language or deliberate applying of certain descriptive means of Poses++.
In order to generate a model representing the philosophers' problem, the objects must be distinguished first, and then their data structures must be specified. The objects involved in the problem described above are 5 philosophers differing from each other and 5 chopsticks also differing from each other.
For every philosopher must be specified which are the chopsticks lying left and right to him. This can be done easily by consecutive numbering of the philosophers and the chopsticks (num: 0..4). The chopstick lying left has the same number as the philosopher. The chopstick lying right has the respectively next higher number. This principle does not work for philosopher 4. On the left he needs chopstick 4 and on the right chopstick 0. This situation results in: left chopstick(num) == num and right chopstick(num) == (num + 1) mod 5. It is obvious that only two philosophers can eat at the same time because more chopsticks are not available.
Next thing to be specified is the situation or status the objects should have. Meditation and eating are the possible states for the philosophers, free or in use are the ones for the chopsticks. When chopsticks are in use, at least one philosopher has the state eating. At the beginning all philosophers have the state meditation, and all chopsticks are free.
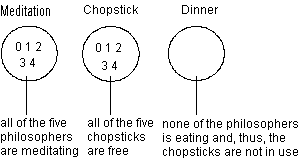
The processes to be modelled are as follows:
"Take both neighboured chopsticks and start to eat"
"Lay the chopsticks after eating and start to meditate".

In order to avoid mutual exclusion of certain philosophers, one philosopher changes from meditation to eating and vice versa. This is implemented on a random basis. Therefore the predicates meditation and eating have the ram access mode (random access). Thus, the "starvation" of certain philosophers is excluded.
The Poses++ system controls the synchronization of the access to the chopsticks (the global ressources in the philosophers model) and, thus, the realization of the critical stage by automatic attempts to fire transitions taking and laying parallel with each other. Thus, a correct state of the model is always guaranteed, no matter whether the fire attempt is successful or not.
Finally deadlocks must be avoided within this model. Such blockings occur when all philosophers simultaneously reach for their left chopsticks and then try to get also a hold of the right ones. In this constellation every philosopher prevents his left neighbour from changing into the status eating. It is easy to understand that a philosopher can take his left chopstick only when his right one is free. Both together is an inseparable action. Also this problem can be solved by means of the Poses++ language concepts. A philosopher changes from the status meditation to the status eating only when all required conditions are met. These conditions are specified by the arc expressions of the transitions taking and laying.
Transition Taking: WHEN a chopstick num is free (1) and the chopstick next to num calculated by (num + 1) mod 5 is free (2) and the corresponding philosopher num is in the status meditation (3) THEN the two chopsticks num and (num + 1) mod 5 are set to in use (1),(2) and change the status of philosopher num from meditation to eating (3),(4) Transition Laying: WHEN a philosopher num has the status eating (5) THEN change the status of him from eating to meditation (5),(6) and set the chopsticks num and (num + 1) mod 5 to the status free (7),(8)
With the help of these rules the arc expressions are formulated in the net design. Despite the complexity of the problem to be modelled the design is complex and clear. Therefore a transformation into the Poses++ source text is relatively formal.
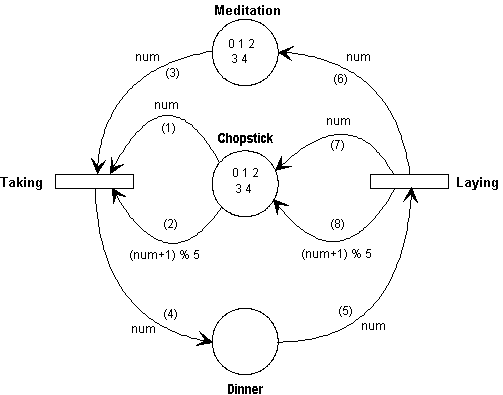
![]()
module Philosopher {
ram<int,5> Meditation << 0 << 1 << 2 << 3 << 4;
/* five philosophers meditate */
ram<int,5> Chopstick << 0 << 1 << 2 << 3 << 4;
/* five chopsticks are free */
ram<int,5> Dinner;
match int num;
trans Taking {
Chopstick >> num; /* (1) */
Chopstick >> (num+1)%5; /* (2) */
Meditation >> num; /* (3) */
Dinner << num; /* (4) */
}
trans Laying {
Dinner >> num; /* (5) */
Meditation << num; /* (6) */
Chopstick << num; /* (7) */
Chopstick << (num+1)%5; /* (8) */
}
};
![]()
|

 |