3.2.3. Arcs

In Poses++ a rule is defined by the arc expressions of a transition according to the following concepts:

Constant Arc Expression
Variable Arc Expression
Arc Expression with Anonymous Variables
Complex Arc Expression
Cardinality of Arcs
Test Arc, Search Arc and Inhibitor Arc
Boolean Conditions
Functions Calls
Timed Arcs

Basically there are input arcs and output arcs. Input arcs describe the relation between transition and predicate on the input. Output arcs describe the relation between transition and predicate on the output.

3.2.3.1. Constant Arc Expression

Constant arc expressions are described the following facts: Find a token which data values exactly match with the constant arc expression.

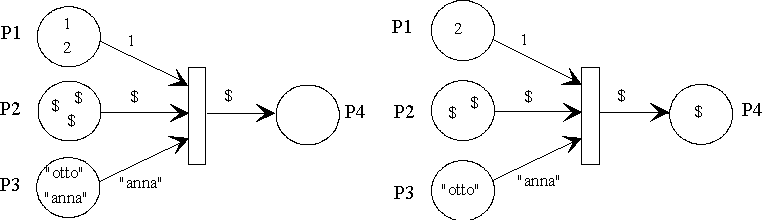
The transition is only allowed to fire, if P1 has at least one token with value 1, P2 at least one $ and P3 at least one "anna", whereas the transition destroys the tokens found, and generates a $ in P4.

module ConstantArcExample {

  fiforam<int,2   >   P1 << 1 << 2;
  place               P2 << card(3), $;
  fiforam<string,2>   P3 << "otto" << "anna";
  place               P4;

  trans T1 {
    P1 >> 1;      // search for a token with value 1
    P2 >> $;      // black tokens are always constant
    P3 >> "anna"; // search for a token with value "anna"

    P4 << $;
  }
};

3.2.3.2. Variable Arc Expression

With constant arc expressions it is possible to establish relations to fixed data. Variable arc expressions are available in case where it is not possible to determine fixed values in advance, for example, in searching for data which shall be related to or which shall meet certain conditions. This type of arc expression is supported by a concept which is called match variables. Match variables have a storage class to which values cannot be assigned explicitely in the way it is possible with normal variables. Match variables can only receive a value in connection with the fire attempts of transitions. The first arc which is utilized by such a variable determines its value from the token which was found first. This value is then considered to be constant for the other arcs of the transition. If, with the help of this constant value no constellation can be found under which the transition fires, the variable is assigned the token value found next in the search sequence of the predicate - which is specified by the access mode - and the procedure will be repeated.

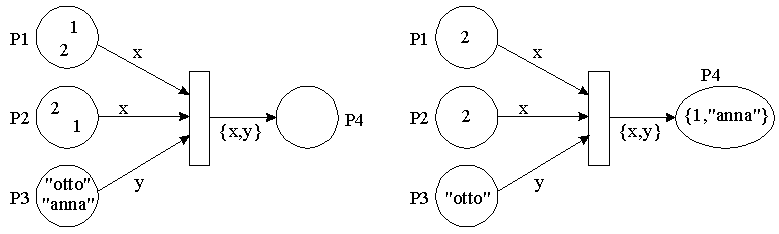
Match variables like x and y can be declared in the scope of a module or in the scope of a transition directly. The difference is only that all transitions can use the match variables declared in the module scope whereas a match variable declared in a transition scope is not visible for other transitions. A scope is always a pair of { ... } like in C or C++ source code.

module VariableArcExample {

  struct IntString {
    int    i;  
    string s;
  };

  fiforam<int      > P1 << 1 << 2;
  fiforam<int      > P2 << 2 << 1;
  lifo   <string   > P3 << "otto"
                        << "anna";
  ram    <IntString> P4;

  match int x; // match variable x in module scope

  trans T1 {

    match string y; // match variable y in transition scope

    P1 >> x;        // search a value in P1 (assign x)
    P2 >> x;        // search the same value of x in P2
    P3 >> y;        // search a string in P3 (assign y)

    P4 << {x,y};    // generate a token with the values of x and y
  }
};

In the example the match variable x is assigned the value 1 by the input arc to P1 because this arc is in the first position within transition T1 and the token with value 1 was filed at first in the predicate by means of the fiforam access mode. Then P2 is investigated for a value 1 in order to meet the condition of the input arc as well. In P3 the arc finds first the string "anna" as specified by the lifo access mode and assigns this string to the match variable y. Thus, the token {1, "anna"} is generated in P4. This fire rule can be described verbally as follows: Find a value in P1 and assign it to match variable x. Find a value in P2 which is identical with the x-value. Then find a string in P3 and assign it to match variable y. Destroy all tokens found and generate a token consisting of the found {x, y} combination for P4.

Note: If the transition is not limited regarding its parallelism, it fires twice immediately because the transition also meets its rule for the combination {2, "anna"}. The x-value which was set to 1 first is not affecting any other transition, not even the same one in its parallel fire attempt.

The use of variable arc expressions implies a certain sequence of the arcs within a transition. The input arc which first occupies a certain match variable assigns it with a value which is constant for the following input/output arcs. If, in the above example, the input arc 1 is placed behind input arc 2, the token {2, "anna"} would be generated in P4 at first. The position of input arc 3 would not matter in this respect but in any case it must be placed in front of the output arc because output arcs can only be described by match variables which have been assigned with a value before.

3.2.3.3. Arc Expression with Anonymous Variables

Certain parts of the token data are not important for variable arc expressions, so they need not be contained in match variable. This is the function of the anonymous variable which is used as a location holder without a value for every type required. Since the anonymous variable does not have a value it can never be used in output arcs because it would'nt remain clearly which token value is to be generated by the output arc.

In the example given the values of the second data entry for all tokens in P2 and P3 are of no importance. These values are characters ´a´ and ´z´ for the tokens of P2, and 22 and 18 for the tokens of P3. Instead of these values the anonymous variable _ is used. The value of that token part which the anonymous variable refers to is not given any attention because there are no interrelations to be matched.

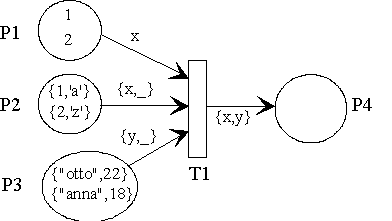
module AnonymousVariableExample {

  struct IntChar   { int    i; char   c; };
  struct StringInt { string s; int    i; };
  struct IntString { int    i; string s; };

  fiforam<int      > P1;
  fiforam<IntChar  > P2;
  fiforam<StringInt> P3;
  fiforam<IntString> P4;

  match int    x;
  match string y;

  trans T1
  {
    P1 >> x;
    P2 >> {x,_};
    P3 >> {y,_};

    P4 << {x,y};
  }
};

Note: The use of the anonymous variables is advantageous for the experiment execution on a simulation server. The simulation server has to execute search processes and comparisons for arcs with constant expressions and expressions containing match variables. Parts of the expression need not be searched and compared when the anonymous variable is used for the reasons mentioned.

3.2.3.4. Complex Arc Expression

In most cases, arc expressions consist of a combination of constant and variable parts. Mathematical expressions are simultaneously used to formulate value relations through match variables as well.

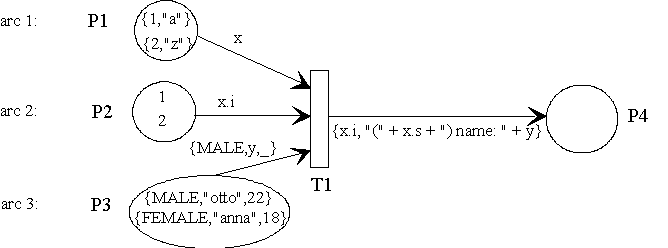
In this example x has the value {1, "a"} from the tokens available in P1. In P2 the token with the corresponding value 1 is found. A token in P3 can only be found when the first token part has the value MALE. The name belonging to it is assigned to y. In P4 the token {1, "(a) name: otto"} is generated. A second parallel fire process is not possible at this time because P3 does not have another token which meets the requirement MALE of the constant arc expression.

module ComplexArcExample {

  struct IntString { int i; string s; };
  enum   Sexes     { MALE , FEMALE    };
  struct Structure { Sexes    mf;
                     string   name;
                     int      num;    };

  fiforam<IntString> P1 << {1,"a"}          << {2,"z"};
  fiforam<int      > P2 <<  1               <<  2;
  fiforam<Structure> P3 << {MALE,"otto",22} << {FEMALE,"anna",18};
  fiforam<IntString> P4;

  match IntString x;
  match string    y;

  trans T1 {
    P1 >> x;               // not yet assigned matchvariable x is
                           // assigned by a token from P1.
    P2 >> x.i;             // assigned matchvariable x (concrete
                           // the int component i) is used as
                           // variable arc description.
    P3 >> {MALE,y,_};      // constant MALE expected and non assigned
                           // string match variable y is assigned

    P4 << {x.i,"("+x.s+") name: "+y}; // result: {1,"(a) name: otto"}
                           // assigned matchvariables x and y
                           // are used for token descriptions
                           // within complex arc expressions.
  }
};

Note: The possibility of creating complex arc expressions is related to the use of valid operators for the types which shall describe the part of the expression. Every part of the expression is represented by an arbitrariliy complex expression. The only exception: a non-assigned match variable can only stand alone for that exact type which is expecting the value assignment. Only after a match variable has been assigned a value, it can be used within other expressions. Such parts of expressions consist of arbitrary combinations of variables, function calls and operators in the form of terms. In the example the string-concat-operator + is used for the string type to describe the token which is to be generated in the predicate P4. The syntax overview in the appendix lists all unary and binary operators which are valid in Poses++.

3.2.3.5. Cardinality of Arcs

In arc expressions, not only the description of the data to be searched for is important but also the number of tokens to be found. This number is called the cardinality of an arc. Poses++ is also able to specify the cardinality of an arc as an expression beside constant cardinalities. In such an expression match variables of the transition may also be used provided that they have already been assigned with a value by another arc. If no cardinality is specified for an arc, the value 1 is implied automatically. No matter how a cardinality is specified, its value must never be smaller than 1. If the cardinality value is 0, the transition cannot fire.

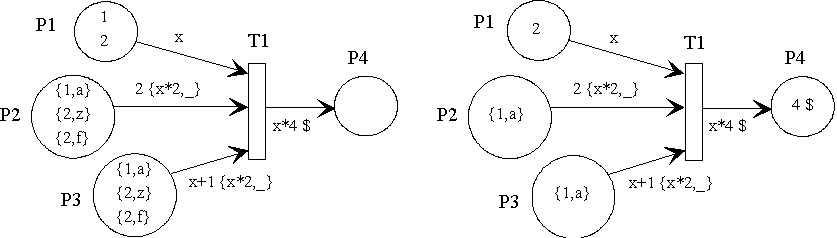
The net fragment shown left formulates the following fire rule: Find a token in P1 and assign its value to x (e.g. value 1). Find two tokens in P2. For both tokens the first token entry shall correspond with the value of the match variable x multiplied by 2 (e.g. value 2). In P3 x+1 (e.g. cardinality 2) tokens shall be found with the same value expression as in the arc of P2. In P4 as many tokens shall be generated as the expression x*4 calculates (e.g. cardinality 4). All these conditions can only be met when the match variable x has the value 1. When this is so, the model situation shown on the right is created.

module CardinalityExample {

  enum   LetterCode { a,f,z };
  struct NumSign    { int i; LetterCode z; };

  fiforam<int    > P1 << 1 << 2;
  fiforam<NumSign> P2 << {1,a} << {2,z} << {2,f};
  fiforam<NumSign> P3 << {1,a} << {2,z} << {2,f};
  place            P4;

  trans T1
  {
    match int x;

    P1 >> x;                  // without card always 1 token
    P2 >> card(2)   ,{x*2,_}; // constant card of 2 tokens
    P3 >> card(x+1) ,{x*2,_}; // variable card of x+1 tokens
    P4 << card(x*4) ,$;       // variable card of x*4 tokens
  }
};

3.2.3.6. Test Arc, Search Arc and Inhibitor Arc

In addition to input and output arcs Poses++ offers three special arcs: the test arc the search arc and the inhibitor arc. The purpose of these arcs is to avoid unnecessary model structures and additional data movements. All these kind of arcs test, search and inhibitor arcs are input arcs of predicates for transitions.

Test arcs behave like input arcs but they do not destroy the found tokens when the transition fires. This this kind of arc will keep found tokens blocked for other test or input arcs. This kind of arc allows you to check whether a special data situation has been reached, without changing it during the fire process. A test arc is represented by the question mark ?.

Transition T1 finds the value 1 in P1 and the suitable value 2 in P2. During the fire process only the token in P1 is destroyed. The token found in P2 remains in P2.

module TestArcExample {

  fiforam<int> P1 << 1 << 2;
  fiforam<int> P2 << 1 << 2;

  trans T1
  {
    match int x;

    P1 >> x;   // find a value in P1 and assign it to x
    P2 ?> 2*x; // find a value x*2 in P2 but do not destroy this token
  }
};

Search arcs work very similar to test arcs but this kind of arc will never keep any token blocked and so a following input or test arc can get and keep this token successfully if not yet kept by another arc before. A search arc is represented by the two character operator ??.

Inhibitor arcs check that no tokens can be found or that a specified number of tokens cannot be found. An inhibitor arc is represented by the two character operator !!. The older operator !> used upto release 1.6 is also available for compatibility reasons.

Transition T1 finds the value 1 in P1. But P2 provides the value 2. So the transition cannot fire with the value found first. The transition then tries to check its rule with value 2 from P1. Since there is no value 4 to be found in P2 the transition can fire and will destroy the value 2 in P1.

module InhibitorArcExample {

  fiforam<int> P1 << 1 << 2;
  fiforam<int> P2 << 1 << 2;

  trans T1
  {
    match int x;
    P1 >> x;   // find a value in P1 and assign it to x
    P2 !> 2*x; // check for non existence of a value 2*x
               // meaning: no value or not 2*x contained
  }
};

In the example shown below the inhibitor arc to P2 means: not 3 (or more) tokens allowed:

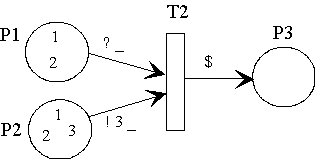
module TestAndInhibitorArcExample {

  fiforam<int> P1 << 1 << 2;
  fiforam<int> P2 << 1 << 2 << 3;
  place        P3;

  trans T2
  {
    P1 ?> _;          /* find a token, the value is unimportant due
                         to the anonymous variable */
    P2 !> card(3), _; /* avoid the existence of in minimum 3 tokens,
                         the values of that tokens are unimportant */
    P3 << $;          // generate one black token
  }
  /*
     in case of T2 can fire this Transition will not affect the
     data situations in P1 and P2 !
  */
};

Since Poses++ release 1.3 unassigned match variables are also allowed for inhibitor arcs. Such an inhibitor arc with a non assigned match variable will use this variable to iterate over the tokens in the corresponding predicate to check for every single token the expression on the inhibitor arc. Only if no token meets the expression the transition depending on such an arc can fire:

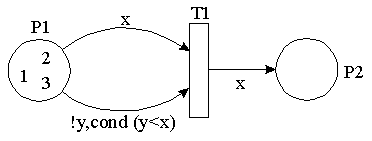
In the examples shown above T1 can fire if it can found a value in P1 to be stored in match variable x whereas no value y in P1 is allowed to match if y<x. The result is a sorted fire sequence.

module InhibitorWithMatchVariableExample {

  fiforam<int> P1 << 1 << 2 << 3;
  fifo   <int> P2;

  match int x,y;

  trans T1
  {
    P1 >> x            // find a value in P1 and assign it to x
       !> y,cond(y<x); // forbid the existence of any value less than x
    P2 << x;
  }
};

Note: In their token expressions input arcs and test arcs can use assigned match variables as well as non-assigned ones, whereas output arcs can only use assigned match variables because these arcs require completely described token values to realize their functionalities.

3.2.3.7. Boolean Conditions

In many cases the combination of constant and variable arc expressions is insufficient to describe the fire rule of a transition. In those cases it is helpful to formulate an additional boolean condition for an arc in order to deliberately limit the tokens to be selected. Only when this condition is also true, the arc has completed its task successfully.

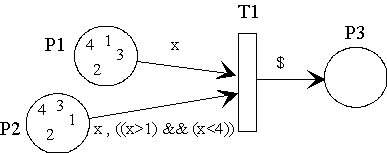
Without the boolean condition on the arc to predicate P2 the transition could fire for every x-value in P1. But the boolean condition specifies that only the values 2 and 3 result in the concession of T1.

module ConditionExample {

  fiforam<int> P1 << 1 << 2 << 3 << 4;
  fiforam<int> P2 << 1 << 2 << 3 << 4;
  place        P3;

  trans T1 {
    match int x;

    P1 >> x;                     // find a value in P1 and assign it to x
    P2 >> x,cond((x>1) && (x<4));// find x, but only if x>1 and x<4
    P3 << $;
  }
};

If it were not possible to formulate the boolean expression in transition 1, the example could only be practiced by means of two transitions. One transition would be searching for the value 2 because - according to the boolean condition - x should be greater than 1. The other transition would be searching for the value 3 because x should be smaller than 4. So the match variable x would not be needed any longer for both transitions. But in case of more complicated constellations the model would require confusing expansions.

All expression syntax known from "C" can be used in a boolean expression. It is advisable to formulate the boolean expression regarding the sequence of arcs as early as possible in order to prevent the simulator from doing unnecessary investigations. Thus, the processing time can be shortened. In the example given the boolean expression could have already been formulated for the arc of P1 because the match variable x already had the correct value there. Additional boolean expressions cannot be formulated for output arcs.

3.2.3.8. Function Calls

Every part of an arc expression can also be expressed by a function, whereas it is important that the return value type of the function corresponds with the type of that expression part which the function is to replace. The type definition is made according to the "C"-conventions.

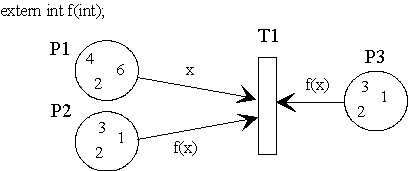
/* C source: e.g. in a user module functest.c

int f(int i) // calculate the half of i
{
  return i/2;
}

*/

// Poses++ source:

int f(int); // function declaration

module FunctionExample {

  fiforam<int> P1 << 2 << 4 << 6;
  fiforam<int> P2 << 1 << 2 << 3;
  fiforam<int> P3 << 1 << 2 << 3;

  match int x;

  trans T1 {
    P1 >> x;    // find a value in P1 and assign it to x
    P2 >> f(x); // find the value in P2 given from the return value of f(x)
    P3 >> f(x); // produce the return value of f(x) as token to P3
  }
};

In the example the extern declared function f provides a value of the type int. Therefore the function can be used for the determination of cardinalities as well as for the formulation of token values, the determination of conditions for boolean expressions etc. But when using functions, it should be considered that the number of function calls made by the simulator for checking the concession is not predictable because this number is determined by the number of search processes for certain tokens in the predicates to be currently evaluated.

Therefore such functions have to have an unambiguous relation between their parameters and their return values. These functions must not have a storing effect. If, for example, a function random instead of f were to be used for the arc expression, the behaviour of the transition and , therefore, of the whole model would no longer be deterministic.

This can be illustrated quite easily: At first value 4 is found in P1 which is assigned to x. The function random(4), when it is called first, provides the random value 3. In P2 the value 3 is found. If then the second call of function random(4) provides the value 0 instead of 3, the arc expression cannot be fulfilled and the transition does not fire.

Basically all C functions can be used provided that their call interfaces have been notified to the Poses++ source text by means of declaration. Match variables can also be used as parameters of functions provided that they have been assigned with a value by other arcs before and that they are of the same type as the expected function parameter.

3.2.3.9. Timed Arcs

In most cases the time regime of transitions is sufficient to reproduce real problems in the model. But sometimes it is reasonable to specify additional time values for individual arcs. The standard time for all input arcs is 0 i.e., the destruction of tokens in the respective input predicates begins at the start of firing of a transition. The standard time for all output arcs is identical with the transition time, so that the generation of tokens in the output predicates is made at the end of the fire process. In case of transitions without time specifications, the start of firing is equal to the end of firing.

Differing from the times determined by the transition, individual times can be specified for each arc. This time specification is always a positive value and relates to the start of firing. Time specifications are not permissible for test and inhibitor arcs because these arcs do not handle a data flow anyway.

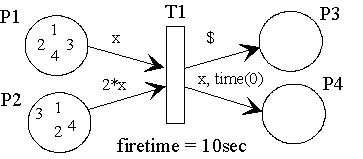
As transition T1 detects its concession, it destroys the tokens found in P1 and P2. A token with the value x in P4 is also generated at this point of time. The black token for P3 will be generated after the transition time is over.

module TimedArcExample {

  fiforam<int> P1 << 1 << 2 << 3 << 4;
  fiforam<int> P2 << 1 << 2 << 3 << 4;
  place        P3;
  fiforam<int> P4;

  trans T1 (firetime = 10sec)
  {
    match int x;
    P1 >> x;            // destroy token immediately
    P2 >> 2*x;          // destroy token immediately

    P3 << $;            // generate token after 10sec
    P4 << x, time(0sec);// generate token immediately
  }
};

copyright © Andrae Behrens 05/24/2023