|
3.2.2. Transitions |
|
Fire
Rule
Actions
Timed
Transitions
Parallelism
Priority
Transition
Properties
Transitions are the active elements of a model. The activity of a transition is called "the transition fire". All concessioned transitions can fire parallel to each other. Also a single transition with more than one concession constellation can fire parallel to itself. How often a transition can fire parallel with itself, whether it shall fire prior to other transitions, or with time delay - is all precisely determined by the definition of the transition.
| 3.2.2.1. Fire Rule | 
|
A transition can only fire when the requirements of its rule are met. So every transition is steadily searching for tokens in order to meet the requirements of its rule which is specified by the adjacent arcs. If a corresponding token constellation has been found, the transition fires. Such constellations are determined by other rules which do not influence the transition criterion directly. They only have a data related influence. This means that a transition fire rule can be completely finished and formulated without any consideration of the global token constellation. Such programming approaches are typical for AI-systems because diverse expert knowledge can be gathered and described independently this way. The formulation of such rules is supported by declaratory languages such as PROLOG. In contradiction to PROLOG in which one rule may also incorporate the observance of another or the same rule recursively, it is not possible with Poses++ to make the observance of one transition fire rule depending on the observance of another transition rule.
A transition fires,
when
|
the capacity of the parallel counter of the transitions is not exhausted yet and |
|
the input predicates of the transition contain enough tokens with the required attributes, whereas number and attributes of the tokens match with the input, test, search and inhibitor arc expressions and |
|
possible boolean conditions which may be formulated for the token attributes of the predicates are fulfilled and |
|
the capacity of output predicates of this transition is sufficient to incorporate as many tokens as required by the cardinality of output arcs. |
then
|
the tokens found in the input predicates are destroyed at the current point of time (on timed input arcs these tokens are destroyed later) and |
|
the tokens to be created for the output predicates are generated after the transition time is over (for timed output arcs are created at arc time regarding transition time). |
Example:
The token constellation in the left part of the net meets the fire rule of transition T1. So, the transition can fire by removing three black tokens from input predicate P1, and generating one black token in output predicate P2 and five black tokens in output predicate P3. The token constellation resulting from that does not allow T1 to fire again because P1 must have at least three black tokens. Such a constellation may arise, for example, when another transition fires for which P1 is the output predicate.
Advice regarding loop constructions:
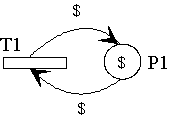According to the above described fire rule, transition T1 cannot fire when
the defined capacity of predicate P1 is 1. This capacity is not sufficient
to incorporate a token as required by the output arc because P1 is already
occupied by another token. However, this token is destroyed by the input
arc at the start of firing, so that exactly at this point of time
and logic the capacity of the predicate would be sufficient to incorporate
another token. The intuitive assumption that transition T1 could fire would
be realistic, if the input arc is treated before the output arc. This
is precisely done in Poses++ for reasons of practical handling. This loop
principle also works when input and output arcs are assigned with separate
fire times and the fire time of the input arc is shorter than or equal to
that of the output arc. The simulation server realizes these fire times only
when they are defined as constant values. It is advisable to avoid loop
constructions with time-dependent arcs as much as possible because variable
fire times of the arcs effect the transition as described above if it does
not meet its fire rule.
| 3.2.2.2. Actions |
|
A transition fire mostly results in a new token constellation. This way a data flow can be represented. Processes to be released by the data flow must be represented by means of the transition description. The detailing degree occurring in the description of such processes requires the ability to implement program operations such as the call of a C/C++ function when activating a transition. Poses++ offers this possibility within the action body of a transition. The action body is defined optionally after the arc expressions of the fire rule.
trans name {
// declarations
// arcs with the fire rule of transition
action { // C code to evaluate at fire start. }
}
If the fire rule of the transition can be met, the action body is realized at the start of firing. This provides the opportunity to do direct programming with the Poses++ modelling language and to include any optional tool into model generation.
An example:
#include "posanim.h"
/*
void Pos_AnimFace (string Tag, // set objects face color to r,g,b
float r,
float g,
float b);
*/
module ActionExample {
buffer<string> tags;
trans transition {
match string tag;
tags >> tag;
action {
// the object face referenced by tag is changed to be red
Pos_AnimFace(tag,1,0,0);
}
}
};
| 3.2.2.3. Timed Transitions |
|
Many processes of the simulation technique require the representation of
the corresponding time behaviour. Poses++ offers the possibility to couple
transitions with a time consuming mode.
The fire time of a transition can be specified as a fixed or calculated time.
A time literal consists of an integer based time value and the
unit of time. For that Poses++ provides
the data type time. The maximum of the time value is 2^53-1 on 32-bit
simulation server machines or 2^64-1 on 64-bit simulation server machines.
The reachable period of time depends on the unit of time. If, for example,
the unit of time is microsecond then the period of time possible
for that model is in minimum142 years. The time base of the simulation kernel
arises from the smallest unit of time of the simulation model. Rounding
errors in time operations cannot occur because the Poses++ simulation kernel
images the simulation time onto an integer data type. Poses++ supports the
following units of time: tic, year, day, hour,
min, sec, millisec (ms), microsec and
nanosec (ns). The unit tic stands for "no unit" and
is in every case equal to the smallest time unit used in the simulation model
(e.g. the smalles unit is millisec than one tic would be equal
to one milli second). In Poses++ is valid: 1year=365days, 1day=24hours,
1hour=60min, 1min=60sec, 1sec=1000millisec, 1millisec=1000microsec,
1microsec=1000nanosec
 |
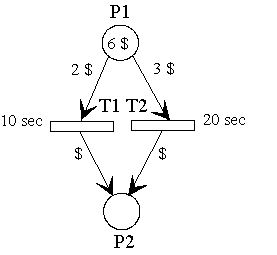The model fragment shown on the left illustrates several possibilities for transitions to fire. T1 and T2 start to fire at time 0. After a simulation time of 10 sec T1 will generate one token, and T2 will generate a token after 20 sec simulation time. After that, none of the transitions would be able to fire again because P1 no longer provides enough tokens. |
#include "posdistr.h" // include the Poses++ distribution function headeer
module FireTimeExample {
place P1 << card(6),$;
place P2;
trans T1 (firetime = 10sec) { // fixed timevalue for firetime of T1
P1 >> card(2),$;
P2 << $;
}
trans T2 {
P1 >> card(3),$;
P2 << $;
action {
// calculated firetime for transition T2
T2.firetime = 1sec * (Pos_Equal(10,20) + Pos_Normal(100,4));
/* the firetime depends on
1 second *
(
(equal distribution between 10 and 20) +
(normal distribution with mean value 100 and deviation 4)
)
*/
}
};
A fixed fire time value can be directly assigned to the attribute or property firetime in the transition head while random time value has to be specified in the action body because it can depend on dynamic data. Thus, it is assured that a new random time value for the transition is set at every point of time that the transition fires.
Poses++ supports the following functions of distribution: equal, normal, logarithmic, gamma, exponential, and poisson distribution. In the appendix all these functions are described. By the programming interface to C the model developer can add other functions as well.
| 3.2.2.4. Parallelism |
|
Transitions work parallel, in principle, because this is the property which allows complex and real problems to be modelled. Another effect is that a transition tries to meet its fire rule as often as possible and to fire parallel with itself. The standard parallelism is set to infinite and has a value of 2^32 -1 = 4294967295 which is sufficient for practical purposes.
 |
Transition T1 fires three times simultaneously because no limitation of parallelism is specified. If the value parallel=2 would be assigned to the transition, it could fire only twice in parallel at first and then one more time (not parallel with itself). But there is no at first and then for transitions without time specification. Therefore a limitation of parallelism is not of importance for these transitions (except their statistics). When a time behaviour (e.g. fixed fire time of 10 sec) is specified for the transition, its time response differs in relation to the statistics: At time 0 two fire processes start simultaneously and run for 10 sec. At this point of time (10 sec) the third firing starts and continues for 10 sec as well (until point of time: 20 sec). |
module ParallelExample {
place P1 << card(6), $;
place P2;
trans T1 (firetime = 10sec, parallel = 2)
{ /* Concession is limited to two parallel fire processes */
P1 >> card(2),$;
P2 << $;
}
};
 |
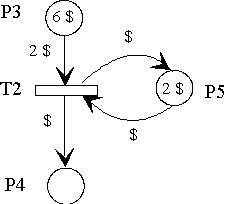The same functionality can be reached by a suitable model structure. For this purpose tokens which act as ressources are used in order to force the maximum parallelism desired. The example shows parallelism value 2 for transition T2. |
module WithoutParallelExample {
place P3 << card(6), $;
place P4;
place P5 << card(2), $; // parallelity is replicate with two operate switches
trans T2 (firetime = 10sec)
{
P3 >> card(2),$;
P5 >> $; // get an operate ressource
P4 << $;
P5 << $; // put an operate ressource
}
};
| 3.2.2.5. Priority |
|
The fact that transitions check their rule parallel in order to fire, often results in a situation several transitions compete with each other for tokens or capacities. As long as no priorities are given for the transition, the competing transitions solve their problems at random i.e., the random number generator decides, with equal chances for all, which of the competing transitions is to be investigated first. If this transition meets the rule, it fires prior to the others which might have been able to fire as well.
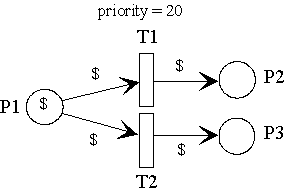
Example of such competitive situations:
If, for example, the transitions T1 and T3 should be continuously preferred, they need higher transition priority values assigned than T2 and T4. The standard transition priority is 0. The lowest possible priority = -2^31. The highest possible priority value = 2^31-1. In any case the simulator investigates all transitions of higher priorities for their concessions first and then those of lower priorities. If several transitions have the same priority, the simulator selects one transition at random (according to the principle of equal distribution) which is to be checked for its concession.
Attention: the understanding for priority values did change in release Poses++ 1.3. All releases before used a standard priority value of 100, a highest priority value 1 and the lowest priority value 2^32-1.
module PriorityExample {
place P1 << $;
place P2, P3;
trans T1 (priority = 20) // priority set to 20 (20 > 0)
{
P1 >> $;
P2 << $;
}
trans T2 // priority of transition T2 is 0 by default
{ // and therefore lower then transition T1
P1 >> $;
P3 << $;
}
// other possibilities to influence the transition priority:
trans T3 (priority = T2.priority - 1)
{
P1 >> $ << $;
}
trans T4
{
P2 >> $ << $;
action {
T4.priority = T4.priority + 1;
// please be careful - the overflow will happen unavoidable !
}
}
};
| 3.2.2.6. Transition Properties |
|
Basides the readonly properties name for the instance name and path for the whole hierarchy of instanciation names every transition has the predefined properties priority, parallel, firetime and life. All these properties are readable and writable. The property priority based on the data type long int specifies the Priority of a transition. The property parallel based on the data type unsigned long int specifies the maximum parallel fire count for a transition. The property firetime specifies the duration of how long the next fire process of a transition should take. A transition with firetime > 0tic is a timed transition but this value can be changed when ever you want.The firetime property is based on the data type time. With the property life the model by itself is able to switch off or to switch on again the transition. A transition switched off will never fire independent from their rule.
module TransitionPropertyExample {
place P;
trans T1 (firetime = 10sec, parallel = 1, priority = 10)
{
P >> $ << card(2),$;
}
trans T2 (firetime = 1sec, parallel = 1)
{
P >> $ << $;
action {
time aTime = T1.firetime; // aTime gets the last fire time of T1
T1.firetime = aTime + 1sec; // T2 changes the fire time for T1 !
T1.parallel = aTime / 1sec; // T2 changes the parallel of T1 !
}
}
};
|
|
